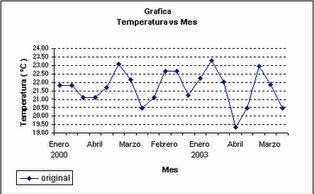
AXIOMAS.

Un evento es el resultado posible un grupo de resultados posibles de un experimento y es la mínima unidad de análisis para efectos de cálculos probabilísticos.

Los eventos se clasifican de la siguiente forma.

 

a.       MUTUAMENTE EXCLUYENTES.

Aquellos que no pueden ocurrir al mismo tiempo

Ejemplo. (Cara o escudo de una moneda)

b.      INDEPENDIENTES

Estos no se ven afectados por otros.

Ejemplo. (el color de zapatos y la probabilidad de que llueva hoy)

c.       DEPENDIENTES.

Cuando un evento afecta a la probabilidad de ocurrencia de otros.

Ejemplo. (Repaso y calificaciones)

d.      NO EXCLUYENTES ENTRE SI.

Cuando la ocurrencia de uno de ellos no impide que ocurra el otro.

Ejemplo. (Que una persona sea doctor y que tenga 56 años.)

 

Cuando el enunciado de un problema de probabilidad tiene como condición que se presenten uno u otro evento la probabilidad total se forma con la suma directa de las probabilidades.

 

P(AOB)=P(A)+P(B)

 

En el caso de eventos no excluyentes entre si debe considerarse que la probabilidad que ocurran ambos eventos esta incluida en ellos esa probabilidad de la suma directa (regla general de la suma de probabilidades.)

 

ARBOL DE LA PROBABILIDAD

Un árbol de probabilidad es una grafica que representa los resultados posibles de un evento asi como la probabilidad de ocurrencia.

 

ESPERANZA MATEMATIA.

Con frecuencia es conveniente calcular que el promedio de los resultados o experimentos, ponderado por la probabilidad de que suceda cada uno de los resultados posibles.

La esperanza matemática permite comprar 2 o mas alternativas.

COMENTARIO

Las axiomas nos demuestran diferentes clases de eventos con los cuales nosotros tenemos posibilidades de resultados y estos pueden ser mutuamente excluyentes, independientes, dependientes y no excluyentes entre si.

EL ARBOL DE LA PROBABILIDAD es una grafica donde se representan todos los resultados posibles de un determinad fenomeno.

ESPACIO MUESTRAL

Se le llama así al conjunto de todos los posibles sucesos elementales es decir un conjunto con todas las soluciones posibles.

 

COMENTARIO

El espacio muestral lo usamos para hacer un arreglo ordenado de todos los resultados posibles que puede generar un fenómeno, el cual nos facilita saber cual de los resultados puede generar.

 

 

COMBINACIONES

El numero de conjunto diferentes, con r elementos cada uno, que puede formarse de un conjunto de n elementos (n>r), se llama combinación de n elementos tomando r a la vez.

Ejemplo.

¿De cuantas formas pueden repetirse seis cartas de una baraja de 52?

 

COMENTARIO

Las combinaciones son un arreglo de objetos sin importar el orden, y la notación que se usa es:

nCr.

 

PROBABILIDAD.

Mide la frecuencia con la que aparece un resultado determinado cuando se realiza un experimento. El experimento  tiene que ser aleatorio, es decir que puede presentarse diversos resultados dentro de un conjunto posible de soluciones.

 

ü  Experimento que es no aleatorio.

Quiere decir que no interviene el azar entonces no lo estudia la probabilidad porque ya sabemos lo que va a pasar.

 

ü  Suceso elemental.

Es la posibilidad que existe de soluciones de un fenómeno. Por ejemplo en un dado hay 6 posibilidades (sucesos elementales)

 

ü  Sucesos compuestos.

En un subconjunto de los sucesos elementales por ejemplo un dado tiene 6 sucesos elementales y que posibilidad hay de que caiga un numero par.

 

 

La probabilidad hace la relación con el numero de resultados de éxito al total de resultados posibles que puede ser subjetiva u objetiva. La primera refleja la percepción de quien la emite y la segunda es el resultado de cálculos.

LA PROBABILIDAD OBJETIVA. Bajo el enfoque clásico supone que todos los eventos tienen la misma probabilidad de ocurrir. Por ejemplo si en una caja existe 50 manzanas y 200 naranjas cual es la probabilidad de que al hacer una extracción  sea una naranja.

Ejemplo

P(N)=          200   .

                200+50

 

P(N)=  0.8= 80% es la posibilidad de agarrar una naranja.

 

PROBABILIDAD SUVJETIVA. Existen naranjas y manzanas.

Si se extrae 80 naranjas de 100 extracciones cual es la probabilidad de que sean naranjas.

 

P(N)= 80

          100

 

P(N)= 0.8=  80%

 

COMETARIO

La probabilidad básicamente nos enseña  y nos demuestra cual es la probabilidad de que suceda determinado fenómeno y para saber o comprobarlo se necesitan de experimentos, y hay 3 clases de experimentos los cuales son: EXPERIMENTO QUE ES NO ALEATORIO, SUCESO ELEMENTAL Y SUSESO COMPUESTO.

PERMUTACIONES

Una permutación es cualquier subconjunto ordenado de un conjunto universal. Es decir se llama permutación de n elementos a los diferentes grupos que pueden hacerse tomándolos todos a la vez.

Una ordenación de numero “R” de dichos objetos, donde “R” es

Existe permutación con repetición.                          EJEMPLO:

P(n;r)=   n!    

             (n-r)!  

COMENTARIO

Nos demuestra que es un arreglo ordenado de objeto, la permutación es la manera como se arregla.

 

TEORIA DEL CONTEO

Análisis combinatorio o técnicas de conteo.

Para establecer el numero de combinaciones o permutaciones en cierto experimento no necesariamente se debe contar en forma directa, existen métodos mucho mas presisos uno de ellos es conocido como “EL PRINCIPIO FUNDAMENTAL DEL CONTEO”. Si un cuento puede efectuarse n1 veces, de manera diferente, entonces otro evento puede efectuarse n2 veces, asi sucesivamente entonces el numero de maneras diferentes que se pueda efectuar el experimento es (n1)(n2)(n3).

COMENTARIO

Básicamente es contar el numero de eventos que cumplen con algún conjunto de condiciones, sirve para calcular la probabilidad de un evento cuando el numero de eventos posibles es muy grande.

CLASES DE TENDENCIA

TNEDENCIA CONSTANTE.

Generalmente esta tendencia debe igualar a cero cuando se tiene esa estimación final. El valor para esta constante suele ser indicativa, de problemas de condicionamiento en datos.

TENDENCIA ESTOCASTICA

La tendencia estocástica también suele llamarse histórica ya que se toma como sucesiones de variables aleatorias, siendo su índice el tiempo, son observaciones tomadas a intervalos iguales con lo cual las aplicaciones visuales corresponden a datos observados cada año, cada mes.

COMENTARIO

LA TENDENCIA CONSTANTE es normal que esta tendencia iguale a cero al final, suele indicar los problemas de condición en la que se encuentran los datos.

LA TENDENCIA ESTOCASTICA    son sucesiones que varían aleatoriamente siendo guiadas por el tiempo y son observaciones con los que podemos saber su valor exacto.

 

SERIES TEMPORALES NO ESTACIONARIAS

Los procesos no estacionarios más comunes son los procesos integrados. Este es un proceso que se caracteriza por que esta integrada en un orden.

También en una serie no estacionaria la media y la variabilidad cambian con el tiempo.

El cambio en la media se traduce la presencia de una tendencia de la serie a crecer o decrecer.

COMENTARIO

En esta la media y la variabilidad cambian con el tiempo, también pueden mostrar un cambio en la media es decir baja o crece por el tiempo.

SERIES TEMPORALES ESTACIONARIAS

Una serie estacionaria es cuando toma valores diferentes en diferentes periodos de tiempo que se repiten, es decir, para datos mensuales, si los valores correspondientes a enero son diferentes a los valores que toma la serie de agosto.

También podemos definir una serie estacionaria como aquella en la que ni la media ni la varianza, ni las cuatro correlaciones dependen del tiempo, una vez estabilizada la serie mediante las transformaciones adecuadas.

COMENTARIO

Básicamente es cuando cambia sus valores a otros en diferentes periodos de tiempo, en esta ni la media, ni la varianza u otro dato depende del tiempo. 

 Series de Tiempo

Una serie temporal o cronológica es un conjunto e observaciones de una variable, ordenadas según transcurre el tiempo.

En una serie de tiempo las observaciones no se deben ordenar de mayor a menor debido a que se perdería el grueso de la información debido a que nos interesa detectar como se mueve la variable en el tiempo es muy importante respetar la secuencia temporal de las observaciones.

 Representación de una Serie Temporal

Par realizar la representación de una serie y temporal se debe realiza mediante una gráfica de dispersión x-y como se muestra en la fig.1

Fig.1. Representación de una serie temporal

 Componetes de una serie temporal

 Tendencia

La tendencia es un movimiento de larga duración que muestra la evolución general de la serie en el tiempo.

La tendencia es un movimiento que puede ser estacionario o ascendente, y su recorrido, una línea recta o una curva. Algunas de las posibles formas son las que se muestran a continuación.

La tendencia es un movimiento que puede ser estacionario o ascendente o descendente como se indica.

Fig. 3 Tendencias ascendente, estacionaria y descendente

También son posibles algunas formas para la tendencia, que no necesariamente tiene una distribución de puntos en forma aproximadamente lineal sino como las que se muestran en la figura.

 Variaciones estacionales.

Se habla de este tipo de variaciones usualmente cuando el comportamiento de la variable en el tiempo en un periodo esta relacionado con la época o un periodo particular, por lo general en el espacio cronológico presente.

 Variaciones cíclicas             

Se llama así a las oscilaciones a lo largo de una tendencia con un periodo superior al año. El ciclo sugiere la idea de que este tipo de movimiento se repite cada cierto periodo con característica parecida. Los ejemplos mas frecuentes se encuentran en le campo de las variables económicas, en estos casos se deben principalmente a la alternancia de las etapas de prosperidad y depresión en la actividad económica.

 

 Variaciones residuales

Cuando a parecen hechos imprevistos, repentinos que afecten las variables en estudio que no podemos proveer nos hallamos frente a variaciones residuales provocadas peores factores externas a aleatorios.

Por ejemplo un día lluvioso y frio durante los veranos es difícil de predecir y aunque perturbaría ciertas actividades diarias como la venta de helados no afectaría en este caso significativamente la serie.

COMENTARIO

Las series temporales también son llamadas históricas o de tiempo donde se muestran datos típicamente ordenados, y se usa para predecir o pronosticar. Las series de tiempo pueden tomar varia formas como: TENDENCIA CRECIENTE, TENDENCIA DECRECIENTE Y TENDENCIA ESTACIONARIA.

REGRESION

La palabra se emplea para denotar el proceso de estimar el valor de una de las variables en función de la otra, cuyo valor se considera dado. Galton fue el primero en utilizar el termino, en un estudio que hizo para relacionar las estaturas de padres a hijos indicando que la estatura de los hijos respecto a de la de sus padres sufre una regresión  a la media, es decir que los hijos de padres con una determinada altura tienen una estatura media mas cercana a la media de la población que a la de sus padres.

Cuando se calcula el valor de X en función de Y, se habla de una regresión de “1 en 2” será cuando calculemos el valor para Y, si conocemos el valor de X.

COMENTARIO

Consiste en predecir los valores de una variable Y conociendo los valores de otra variable X.

Vimos que la fuerza de una correlación entre X y Y aumenta a medida que los puntos del diagrama de dispersión se estrechan formando una línea recta imaginaria. Esta línea la podemos identificar con una línea de regresión, línea recta que se dibuja a través del diagrama de dispersión.

 

CORRELACION LINEAL

El coeficiente de correlación lineal r es la media numérica de la intensidad de la relación lineal entre dos variables. Se llama lineal porque la representación grafica de Y es una recta.

COEFICIENTE DE CORRELACION DE PEARSON

Es una medida que indica la situación relativa de los mismos sucesos respecto a las dos variables y son números que están entre los límites +1 y-1.

Para medir la relación entre dos variables se calcula el coeficiente de correlación lineal r.

INTERPRETACION DE UNA CORRELACION

Para interpretar un coeficiente de correlación hay que tener en cuenta por un lado su magnitud y por otro su signo. La magnitud se refiere al grado en que la relación entre las dos variables queda bien descrita con r, mientras que el signo se refiere al tipo de relación.

Un coeficiente de correlación positivo entre las variables  X  e  Y, indica la tendencia a aumentar los valores de Y cuando aumentamos los de X y a disminuir los valores de Y cuando disminuimos los de X.

Un coeficiente de correlación negativo indica tendencia a disminuir los valores de Y cuando aumentamos los de X y aumentar los de Y cuando disminuimos los de X.

Un coeficiente de correlación en torno a cero indica que el modelo de relación lineal entre esas variables no es valido. Que cuando aumentamos X, Y puede indistintamente aumentar o disminuir.

Por la magnitud del coeficiente de correlación decimos que si el modulo del coeficiente de correlación se sitúa entre 0 y 0.20, entonces es insignificante, si esta entre 0.20 y 0.50 medio, entre 0.50 y 0.80 alto y a partir de 0.80 muy alto.

comentario

Por correlación entiendo que es una forma de medir la intensidad o grado de relación que existe entre dos variables nos ayuda a entender en que forma se relacionan dos 

TEOREMA DE SHEPPARD
En este teorema se utiliza la formula de la varianza corregida.
Segun cientificos el teorema de sheppard no es muy utilizada mientras otros opinan que si es necesario utilizarla ya que corrige ciertos errores en el proceso y aplicacion de la amplitud.

por ejemplo si en la columna de frecuencias existen ceros, la o las filas que contienen ese cero se eliminan automaticamente y se corre la siguiente fila hacia arriba aunque parezca incorrecto por la alteracion de la aplicacion de la amplitud eso es lo correcto.

COMENTARIO
Este teorema tambien tiene por objetivo corregir la varianza en criterios de comparacion con otra tabla o de datos o de distribucion.

RELACION ENTRE DIAGRAMA DE CAJAS Y AREA BAJO LA CURVA

La relacion que existe entre el diagrama de cajas "Box plot" y area bajo la curva es que las dos graficas nos muestrn o representan en que parte de los mismos se encuentran ubicada la media y la mediana, estas graficas llevan una estrecha relacion ya que las dos graficas las utilizamos para por representar los datos de una distribucion.

COMENTARIO:
El box plot y area bajo la curva son dos temas importantes que utilizamos en estadistica porque en estadistica formamos tablas de ditribucion de datos y estas dos graficas nos ayudan a representar estos datos.

CARACTERISTICAS DEL BOX PLOT

- La distribucion de datos se dispersan mas cuando la caja se hace mas largo.
- Esta grafica puede rpresentarse horizontal y verticalmente
- La media se representa por una linea que divide en dos partes iguales a la distribucion y a la caja.
- La media puede coincidir con los cuartiles.

COMENTARIO
El box plot o diagrama de cajas representa varias caracteristicas las cuales pueden diferenciarla o ya sea relacionarla con la grafica de curva normal.

DIAGRAMA DE CAJAS O “BOX PLOT”

Permite identificar con claridad y de forma individual, observaciones que se alejan de manera poco usual del resto de los datos. A estas observaciones se les conoce como valores atípicos.Por su facilidad de construcción e interpretación, permite también comparar a la vez varios grupos de datos sin perder información ni saturarse de ella. Esto ha sido particularmente importante a la hora de escoger esta representación para mostrar la opinión de los estudiantes respecto a la actuación docente a través de las diversas preguntas del instrumento utilizado.
Partes del Boxplot: El nombre original del gráfico introducido por Jhon Tukey en 1977 es Box and whisker plot, es decir, diagrama de caja y bigote. En efecto, el gráfico consiste en un rectángulo (caja) de cuyos lados superiores e inferior se derivan respectivamente, dos segmentos: uno hacia arriba y uno hacia abajo (bigotes).La caja y los bigotes están ubicados paralelos a un eje rotulado, que en este caso está en la escala del 1 al 5 e indica el puntaje obtenido en una pregunta según la opinión de los estudiantes que llenaron el instrumento de opinión.Las partes del Boxplot se identifican como sigue:1.-Límite superior: Es el extremo superior del bigote. Las opiniones por encima de este límite se consideran atípicas. Para más detalles consulte sobre la construcción de los límites y los valores atípicos.2.-Tercer cuartil (Q3): Por debajo de este valor se encentran como máximo el 75% de las opiniones de los estudiantes.3.-Mediana: Coincide con el segundo cuartil. Divide a la distribución en dos partes iguales. De este modo, 50% de las observaciones están por debajo de la mediana y 50% está por encima.4.-Primer cuartil (Q1): Por debajo de este valor se encuentra como máximo el 25% de las opiniones de los estudiantes5.-Límite inferior: Es el extremo inferior del bigote. Las opiniones por debajo de este valor se consideran atípicas. Para más detalles consulte sobre la construcción de los límites y los valores atípicos.6.-Valores atípicos: Opiniones que están apartadas del cuerpo principal de datos. Pueden representar efectos de causas extrañas, opiniones extremas o en el caso de la tabulación manual, errores de medición o registro.Se colocan en la gráfica con asteriscos (*) o puntos (.) según se alejan menos o más del conjunto de datos. Se utiliza un superíndice numérico para indicar el número de veces que aparece ese dato como atípico. NOTA: Esta presentación en línea del Boxplot está en primera versión y aun en proceso de mejora. Se señalan los datos atípicos con una circunferencia (o) en el caso de ser única la observación. En caso contrario, usted sólo verá un triángulo ($). Si esto sucede, debe remitirse al reporte numérico para verificar la cantidad de observaciones atípicas por pregunta.7.-Media aritmética: Es lo que tradicionalmente se conoce como promedio. Originalmente no forma parte del boxplot, sin embargo, se consideró su inclusión para dar una idea del puntaje general obtenido por pregunta. Actualmente se trabaja en la elaboración de estadísticos más representativos que la media aritmética para describir el conjunto de datos.¿Cómo se interpreta? Tenga en cuenta las siguientes consideraciones a la hora de interpretar el boxplot:.-Mientras más larga la caja y los bigotes, más dispersa es la distribución de datos..-La distancia entre las cinco medidas descritas en el boxplot (sin incluir la media aritmética) puede variar, sin embargo, recuerde que la cantidad de elementos entre una y otra es aproximadamente la misma. Entre el límite inferior y Q1 hay igual cantidad de opiniones que de Q1 a la mediana, de ésta a Q3 y de Q3 al límite superior. Se considera aproximado porque pudiera haber valores atípicos, en cuyo caso la cantidad de elementos se ve levemente modificada..-La línea que representa la mediana indica la simetría. Si está relativamente en el centro de la caja la distribución es simétrica. Si por el contrario se acerca al primer o tercer cuartil, la distribución pudiera ser sesgada a la derecha (asimétrica positiva) o sesgada a la izquierda (asimétrica negativa respectivamente. Esto suele suceder cuando las opiniones de los estudiantes tienden a concentrase más hacia un punto de la escala..-La mediana puede inclusive coincidir con los cuartiles o con los límites de los bigotes. Esto sucede cuando se concentran muchos datos en un mismo punto, en este caso, cuando muchos estudiantes opinan igual en determinada pregunta. Pudiera ser este un caso particular de una distribución sesgada o el caso de una distribución muy homogénea..-Las opiniones emitidas como No aplica (N/A) cuando en realidad sí aplica o las opiniones nulas (cuando el estudiante no opina en una pregunta), no son tomadas en cuenta para elaborar el boxplot de esa pregunta. Por esta razón encontrará que en ocasiones no hay igual número de opiniones para todas las preguntas..-Debe estar atento al número de estudiantes que opina en cada pregunta. Lo que pareciera ser dispersión en los resultados, en ocasiones podría deberse a un tamaño de muestra muy pequeño: pocos estudiantes opinaron. Debe ser cauteloso a la hora de interpretar. En estos casos se sugiere remitirse al reporte numérico..-En términos comparativos, procure identificar aquellas preguntas cuyos boxplot parecen diferir del resto. Pudiera con esto encontrar fortalezas o debilidades en su actuación según la opinión de los estudiantes.Se observa una variabilidad muy grande en cuanto a las impresiones que los estudiantes tienen del profesor en los diferentes aspectos de su actuación. Esto se concluye porque no existe una tendencia homogénea en las respuestas por pregunta.Las opiniones son muy homogéneas y positivas en la pregunta 5: Logra comunicarse efectivamente con el estudiante. Este aspecto resalta en la actuación del docente y además todos los estudiantes encuestados coinciden en ello.También se considera muy positiva la impresión que los estudiantes tienen en cuanto a los aspectos que se refieren a las preguntas 2, 6, 9, 12 y 13; salvo un par de opiniones que difieren del resto en las preguntas 2 y 6, las respuestas son homogéneas. Note que estas opiniones separadas son datos atípicos pues se alejan del cuerpo de datos. Note también que por el proceso de mejora que sufren los gráficos presentados en línea, debe remitirse al reporte numérico en la pregunta 2 para verificar el número de respuestas atípicas dado que el símbolo representativo por el momento es ($), mas no así en la 9 pues ya se comentó que el símbolo (¡) se refiere a sólo un dato atípico y en este caso vale “2”.Observe que según la opinión de los estudiantes el aspecto de la pregunta 17: Realiza la entrega y revisión oportuna de los resultados de las evaluaciones revela el puntaje más bajo respecto al resto de las pregunta, lo cual pudiera ser un aspecto a considerar por el docente dado que además el 50% de los estudiantes le otorga el puntaje más bajo. Note que aquí la mediana es “1”, lo que indica que la mitad de las observaciones está allí (no por debajo porque no hay valor más bajo)Note que algunos boxplot no tienen bigotes. En estos casos, como por ejemplo en la pregunta 19, el límite inferior coincide con el Q1 y el límite superior coincide con el Q3. En esta pregunta se evidencia simetría y bastante variabilidad.El resto de las preguntas presentan alta variabilidad por lo que deben leerse cuidadosamente en función del punto donde se concentra la mayor cantidad de información, esto es, viendo la posición de la mediana (véase Simetría). Esta alta variabilidad indica que la opinión de los estudiantes respecto a los planteamientos es bastante heterogénea.
GlosarioCuartiles: Son valores que dividen a la distribución en cuatro partes iguales en cuanto a la cantidad de datos. Así, tenemos que el Primer cuartil (Q1), es el valor por debajo del cual ocurre el 25% de las observaciones y el Tercer cuartil (Q3) es aquel por debajo del cual ocurre el 75% de las observaciones. Siguiendo en esta línea, el Segundo cuartil (Q2) coincide con la mediana de la distribución.
Dispersión: Indica la variabilidad del conjunto de datos: cómo se distribuyen los datos de estudio. Una dispersión grande indica un conjunto de datos heterogéneos e implica poca utilidad de una medida de tendencia central únicamente para describir la distribución.Estadísticos: son valores representativos que proporcionan información sobre la serie en cuanto a su posición en la escala de medición, agrupamiento en torno a un valor, distribución de los datos y concentración en una región entre otros. Los estadísticos proveen información sobre una muestra. Cuando se trabaja con toda la información (población) se le denomina parámetro.
Mediana: Es medida de tendencia central. Es un dato de la distribución que la divide en dos partes iguales de forma tal que por debajo y por encima de ella se encuentra como máximo el 50% de los datos de estudio. Por ejemplo, si las opiniones de cinco estudiantes (en puntaje del 1 al 5) fueron: 1-1-3-4-5, entonces 3 es la mediana; o si los puntajes fueron: 1-1-3-4-5-5, la mediana está entre 3 y 4 y la consideramos como 3,5.
Media aritmética o promedio: Es un estadístico de tendencia central. Representa una especia de punto de equilibrio para el conjunto de datos. Para calcularlo se emplean todos los datos de la distribución por lo que tiene la desventaja de verse afectada por datos muy grandes o pequeños, lo que conlleva a que en ocasiones no sea representativa de la distribución. Resulta de sumar todos los datos de la distribución y dividirlos entre el total de datos.
Simetría: Indica la forma del conjunto de datos, lo cual implica observar dónde se concentra la información. Para el estudio de la forma de una distribución, también se usan los términos sesgo o asimetría. Una distribución puede ser:
.-Simétrica: en este tipo de distribuciones la media, la moda y la mediana coinciden y los datos se distribuyen de igual forma a ambos lados de estas medidas. En el contexto, hay igual número de opiniones por encima que por debajo de la mediana.
.-Asimétrica positiva o sesgada a la derecha: los datos tienden a concentrarse hacia la parte inferior de la distribución y se extienden más hacia la derecha. Sobre la construcción de los límites y los valores atípicosTukey (1997) sugiere una regla sencilla para determinar los límites de los bigotes. Tomando en cuenta que el Rango Intercuartílico (RI) es la diferencia entre el Tercer y el Primer Cuartil, tenemos que existen límites interiores y límites exteriores. Los primeros son barreras hasta las cuales se “permiten” datos de la muestra, por estar muy cerca del resto. Estos son los límites que definen los extremos de los bigotes. De sobrepasar esta barrera se le considera valor atípico. Los segundos límites indican cuándo un dato se aleja en exceso del resto y, siendo también atípico, se le considera fuera del límite exterior permitido y se dice que es aún más atípico.Se construyen así:Límite interior inferior = Límite del bigote inferior = Q1 - 1,5RILímite interior superior = Límite del bigote superior = Q3 + 1,5RILímite exterior inferior = Q1 - 3RILímite exterior superior = Q3 + 3RI

ejemplos de diagrama de cajas

COMENTARIO:
El diagrama de cajas es otra tecnica utilizada en estadistica para representar los datos encontrados en una distribucion de datos esta grafica nos ubicara lo siguiente:
cuartil 3, cualtil 2, cuartil 1, media y con los cuartiles 1 y 3 sacaremos el rango intercuartilico (RIT) para poder encontrar la ubicacion de los bigotes y la barrera interior y exterior.

VALORES ESTANDARIZADOS:
Como sabemos la curva normal de frecuencias tiene forma de campana en cuyo centro se ubican tres medidas de tendencia central (media, moda y mediana) en particular el promedio o media aritmetica es la medida que representa un universo muestral mientras a los datos de este valor se encuentran valores mas altos y mas bajos aproximadamente la mitad para cada lado y se dipersan segun la desviacion estandar.

COMENTARIO
Los valores estandarizados nos ayudan a encontrar el valor de "z" en la que se utiliza la siguiente formula: z es igual a incognita menos la media o el promedio de la muestra dividido entre la desviacion estandar.

PORTAFOLIOS

Muchos educadores han aportado definiciones, veamos algunas de ellas:
Un portafolio es un registro del aprendizaje que se concentra en el trabajo del alumno y su reflexión sobre esa tarea. Mediante un esfuerzo cooperativo entre el alumno y el personal docente se reúne un material que es indicativo del progreso hacia los resultados esenciales (National Education 1993).
Un Portafolio es una selección deliberada de los trabajos del alumno que nos cuenta la historia de sus esfuerzos, su progreso o sus logros. En él deben incluirse la participación del alumno en la selección de su contenido, los criterios de la selección y las pautas para juzgar sus méritos, así como las evidencias de su proceso de reflexión (Arter, 1990)
Un portafolio es algo más de una mera “caja llena de cosas”. Se trata de una colección sistemática y organizada de evidencias utilizadas por los maestros y alumnos para supervisar la evolución del conocimiento, las habilidades y las actitudes de estos últimos en una materia determinada
Un portafolio desde la perspectiva educativa es un procedimiento de producción,que permiten recopilar productos de proyectos de curso, variados escritos, grabaciones y otras muestras de acciones y creaciones de los alumnos.

COMENTARIO
Un portafolio es una selección deliberada de los trabajos de un alumno que en cierta forma nos cuenta la historia de sus esfuerzos, su progreso y sus logros

COMENTARIO
el area bajo la curba esta compuesta por la curva y por la linea base entre las cuales se encuentran el conjunto de desviaciones situadas entre ellas.

AREA BAJO LA CURVA NORMAL

La distribución normal fue reconocida por primera vez por el francés Abraham de Moivre (1667-1754). Posteriormente, Carl Friedrich Gauss (1777-1855) elaboró desarrollos más profundos y formuló la ecuación de la curva; de ahí que también se la conozca, más comúnmente, como la "campana de Gauss". La distribución de una variable normal está completamente determinada por dos parámetros, su media y su desviación estándar, denotadas generalmente por y . Con esta notación, la densidad de la normal viene dada por la ecuación:
Ecuación 1:
que determina la curva en forma de campana que tan bien conocemos . Así, se dice que una característica sigue una distribución normal de media y varianza , y se denota como , si su función de densidad viene dada por la Ecuación 1.
Al igual que ocurría con un histograma, en el que el área de cada rectángulo es proporcional al número de datos en el rango de valores correspondiente si, tal y como se muestra en la Figura 2, en el eje horizontal se levantan perpendiculares en dos puntos a y b, el área bajo la curva delimitada por esas líneas indica la probabilidad de que la variable de interés, X, tome un valor cualquiera en ese intervalo. Puesto que la curva alcanza su mayor altura en torno a la media, mientras que sus "ramas" se extienden asintóticamente hacia los ejes, cuando una variable siga una distribución normal, será mucho más probable observar un dato cercano al valor medio que uno que se encuentre muy alejado de éste.
Figura 1. Histograma de los valores de tensión arterial sistólica para dos muestras de pacientes isquémicos ingresados en una unidad de cuidados intensivos.
Figura 1a.- Valores de tensión arterial sistólica en una muestra de 1000 pacientes isquémicos ingresados en UCI.
Figura 1b.- Valores de tensión arterial sistólica de una muestra de 5000 pacientes ingresados en UCI.
TABLA DE AREA BAJO LA CURVA figura 2

CODIFICACION
La codificación de caracteres es el método que permite convertir un carácter de un lenguaje natural (alfabeto o silabario) en un símbolo en otro sistema de representación, como un número o una secuencia de pulsos eléctricos en un sistema electrónico, aplicando normas o reglas de codificación

EL DIAGRAMA DE TALLO Y HOJA

Es una técnica estadística para representar un conjunto de datos. Cada valor numérico se divide en dos partes. El o los dígitos principales forman el tallo y los dígitos secundarios las hojas. Los tallos están colocados a lo largo del eje vertical, y las hojas de cada observación a lo largo del eje horizontal.

Ejemplo
La siguiente distribución de frecuencia muestra el número de anuncios comerciales pagados por los 45 miembros de Greater Buffalo Automobile Dealer´s Association en 1999. Observemos que 7 de los 45 comerciantes pagaron entre 90 y 99 anuncios (pero menos de 100). Sin embargo, ¿El numero de comerciantes pagados en esta clase se agrupan en alrededor de 90, están dispersos a lo largo de toda clase, o se acumulan alrededor de 99? No podemos saberlo.

# De anuncios comprados Frecuencia
80 a 90 2
90 a 100 7
100 a 110 6
110 a 120 9
120 a 130 8
130 a 140 7
140 a 150 3
150 a 160 3
Total 45


Una técnica que se usa para presentar información cuantitativa en forma condensada es el diagrama de tallo y hoja. En el ejemplo anterior no podíamos la identidad de los valores de la clase de 90 a 100. Para ilustrar la construcción de un diagrama de tallo y hojas usando el número de comerciales comprados, supongamos que las 7 observaciones en la clase de 90 a 100 sean 96, 94, 93, 94, 95, 96, 97. EL valor de tallo es el digito o dígitos principales, en este caso el 9. Las hojas son los dígitos secundarios. EL tallo se coloca a la izquierda de una línea vertical y los valores de las hojas a la derecha.

Medidas de Dispersión
Se llaman medidas de dispersión aquellas que permiten retratar la distancia de los valores de la variable a un cierto valor central, o que permiten identificar la concentración de los datos en un cierto sector del recorrido de la variable. Se trata de coeficiente para variables cuantitativas. A) El desvío estándarEs posible identificar conjuntos de datos que a pesar de ser muy distintos en términos de valores absolutos, poseen la misma media. Una medida diferencial para identificar esos conjuntos de datos es la concentración o dispersión alrededor de la media.
Los valores de las clases de 90 a 100, aparecerían como sigue:9 6 4 3 4 5 6 7 Por ultimo, ordenamos los valores dentro de cada tallo de menor a mayor. El segundo renglón del diagrama de tallo y hojas aparecería como sigue:9 3 4 4 5 6 6 7 Con el diagrama de tallo y hojas podemos observar rápidamente que hubo 2 comerciantes que compraron 94 comerciales y que el número de anuncios comprados fue desde 93 hasta 97. Un diagrama de tallo y hojas es semejante a una distribución de frecuencia, pero con más información, esto es, valores de datos en lugar de marcas.

F) Rango intercuartílico:El rango intercuartílico RI es, sencillamente, la diferencia entre el tercer y el primer cuartil, es decir

VARIABLE:
Una variable es un simbolo que representa un elemento no especificado de un conjunto dado. Dicho conjunto es llamado conjunto universal de la variable o universo de la variable, y cada eLas variables pueden ser cualitativas o cuantitativas.

VARIABLES CUALITATIVAS: aquellas que no aparecen en forma numérica, sino como categorías o atributos (sexo, profesión, color de ojos) y sólo pueden ser nominales u ordinales.

variables nominales: lo único que puede hacerse es establecer frecuencias en cada atributo y la igualdad o desigualdad entre los diferentes casos, ver cuál es el grupo que tiene mayor frecuencia alcanzando el concepto de “moda” (y también obtener algunas medidas de asociación cuando se relacionan variables entre sí).

variables ordinales: recogen la idea de orden pero no tiene sentido realizar operaciones aritméticas con ellas (acuerdo o desacuerdo con un proyecto de ley) ya que no puede medirse distancia entre una categoría y otra. Se puede establecer aquí igualdad y desigualdad, y relaciones como mayor que, y menor que. Puede establecerse orden, pero no medirse distancia dentro de ese orden. La medida estadística de tendencia central más apropiada para estas escalas es la "mediana".lemento del conjunto es un valor de la variable.

VRIABLE CUANTITATIVA:Aquella que se puede medir y se expresa numéricamente. Estos números reciben el nombre de datos. Los caracteres cuantitativos son de dos tipos:
Discretos: toman un número determinado de valores.
Continuo: Pueden tomar cualquier valor comprendido entre dos valores dados. Estos datos se agrupan en intervalos.

MEDIDAS DE TENDENCIA CENTRAL

La Media Aritmética
La medida de tendencia central mas ampliamente usada es la media aritmética, usualmente abreviada como media.
La media aritmética de un conjunto de n valores es el resultado de la suma de todos ellos dividido entre n.
Propiedades de la media aritmética
1. Puede ser calculada en distribuciones con escala relativa e intervalar.
2. Todos los valores son incluidos en el cómputo de la media.
3. Una serie de datos solo tiene una media.
4. Es una medida muy útil para comparar dos o más poblaciones.
5. Es la única medida de tendencia central donde la suma de las desviaciones de cada valor respecto a la media es igual a cero. Por lo tanto podemos considerar a la media como el punto de balance de una serie de datos.

Moda
Es el dato que más se repiten en la cuenta. Si existen dos datos que se repite un numero igual de veces entonces el conjunto será bimodal. Ejemplo:
Numero de personas en distintas casas en una villa:
5-7-4-6-9-5-6-1-5-3-7
en este caso el numero que más se repite es 5 entonces la moda en este caso es 5.

Mediana
Definiremos como mediana al valor de la variable que deja el mismo número de datos antes y después que él.
De acuerdo con esta definición el conjunto de datos menores o iguales que la mediana representarán el 50% de los datos, y los que sean mayores que la mediana representarán el otro 50% del total de datos de la muestra.
Matemáticamente hablando la mediana sería: Me =n+1/2 , si n es impar --> Me será la observación central de los valores, una vez que estos han sido ordenados en orden creciente o decreciente.

ESTADISTICA

Rama de la matematica que se encarga de ordenar y calcular datos.